よくわかる！金融用語辞典　【IS曲線】

ＩＳ曲線は、財市場の均衡を示す利子率と国民所得の組み合わせを表す右下がりの曲線で、「利子率が上がると国民所得が減少し、利子率が下がると国民所得が増加する」という関係を表します。

 

ＩＳ曲線のＩは投資、Ｓは貯蓄を示し、ＩＳ曲線は財市場の均衡（投資Ｉ＝貯蓄Ｓ）を意味します。

 

 

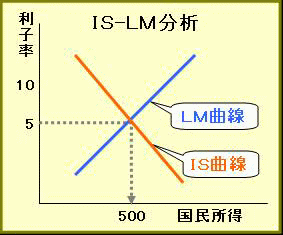
（注）説明をやさしくするために、図には直線を表示しています。なお、直線は、曲線の一種です。

 

≪財市場の超過供給と超過需要≫

 

ＩＳ曲線は、財市場の貯蓄（供給の基本要因）と投資（需要の基本要因）の均衡を示す利子率と国民所得の組み合わせの線分です。ＩＳ曲線上以外の領域では、財市場は均衡していません。

 

ＩＳ曲線より上方では、財市場は超過供給の状態にあります。一方、ＩＳ曲線より下方では、財市場は超過需要の状態にあります。

 

 

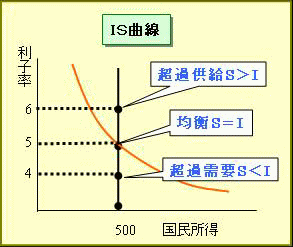
≪ＩＳ曲線の形状≫

 

ＩＳ曲線は、簡単に直線で表示（直線近似という）することができます。ＩＳ曲線の傾きは、投資の利子弾力性によって、水平（０度）から垂直（９０度）まで変化します。

 

投資の利子弾力性が大きいと、小さな利子率の変化に投資が大きく反応して、国民所得が大きく変化します。投資の利子弾力性が無限大（∞）に大きい場合には、ＩＳ曲線はほぼ水平になります。

 

逆に、投資の利子弾力性が小さいと、大きな利子率の変化にも投資が反応しなくなり、国民所得も影響を受けなくなります。投資の利子弾力性が限りなくゼロに近い場合には、ＩＳ曲線はほぼ垂直（急勾配）になります。

 

 

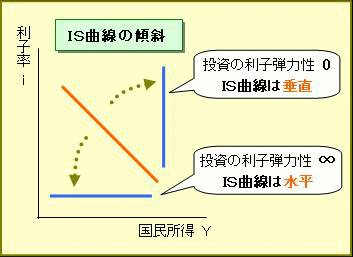
≪ＩＳ曲線式≫

 

ＩＳ曲線を表す数式のことを「ＩＳ曲線式」と呼ぶことにします。ＩＳ曲線式は、財市場の均衡（総供給＝総需要）を表す「国民所得Ｙ＝消費Ｃ＋投資Ｉ＋政府支出Ｇ」という関係式を「利子率ｉ」について解いた（計算式を「ｉ＝～」の形にする）ものです。

 

◆租税を考慮しない場合

 

所得均衡式「Ｙ＝Ｃ+Ｉ+Ｇ」に、消費関数として「Ｃ＝α＋βＹ」を、投資関数として「Ｉ＝Ｉ₀－ｂｉ」を代入し、利子率ｉについて解くと、次のようになります。

 

 

α：基礎消費、β：限界消費性向、Ｉ₀：独立投資、ｂ：投資の利子弾力性、ｉ：利子率、Ｙ：国民所得、Ｇ：政府支出

 

◆租税を考慮する場合

 

所得均衡式「Ｙ＝Ｃ+Ｉ+Ｇ」に、消費関数として「Ｃ＝α＋βＹ」を、投資関数として「Ｉ＝Ｉ₀－ｂｉ」を、租税関数として「Ｔ＝Ｔ₀＋ｔＹ」を代入し、利子率ｉについて解くと、次のようになります。

 

 

Ｔ₀：最低課税額（独立租税）、ｔ：限界租税性向

 

上記の式の－(１－β＋βt）/ｂは、勾配（こうばい：傾斜のこと）を表します。この勾配のマイナス符号は、ＩＳ曲線が右下がりの曲線であることを表しています。一方、（α+Ｉ₀+Ｇ－βＴ₀）/ｂ は、縦軸の切片（せっぺん）を表します。

 

財政政策で政府支出（Ｇ）を増やすと、切片の数字が大きくなり、ＩＳ曲線は上方に平行移動します。

 

※ここでは、投資関数を簡単な一次式で表しています。

スポンサーリンク

金融大学TOP > よくわかる！金融用語辞典 > IS曲線