よくわかる！金融用語辞典　【ウィーナー過程】

 

ウィーナー過程とは、ブラウン運動が作りだす確率過程です。原資産の動きの予測モデルには、一般化したウィーナー過程を利用しています。

 

≪ウィーナー過程とブラウン運動≫

 

１８２７年、イギリスの植物学者ロバート・ブラウンは、水に浮かべた花粉の微粒子が、まるで生き物のように震動していることに気付きました。この不思議な動きは時間とともに複雑性を増していきます。この粒子の運動過程をブラウン運動といいます。

 

ブラウン運動が作りだす確率過程のことをウィーナー過程といいます。確率過程とは、時間とともに推移する確率現象の数学的モデルのことで、確率とは、ある出来事が起こり得る可能性の度合いのことをいいます。

 

≪オプション価格の計算≫

 

オプション価格を決めるには、原資産の価格変動の振る舞いを予測することが必要です。オプションでは、原資産価格の動きに、一般化したウィーナー過程という確率過程を仮定しています。

 

◆一般化したウィーナー過程

 

一般化したウィーナー過程とは、ウィーナー過程にドリフト項（基本的な方向性）を合わせたもので、「酔っ払いの千鳥足」の動きに例えられます。酔っ払いが家路に向かうとき、左右にフラフラとよろけながら、家のある方向に歩きます。酔っ払いの千鳥足は、一定方向へ向かう動きとフラフラする動きからなっています。

 

◆ドリフト項

 

原資産価格の動きには、不安定な動きだけではなく、基本的な方向性を示す確定的な動きも見られます。この基本的な方向性を示す部分をドリフト項といいます。

 

◆ウィーナー過程

 

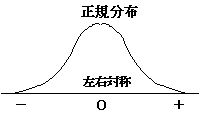
ウィーナー過程は、酔っ払いのフラフラした動きに相当します。酔っ払いの程度によってフラフラする足取りが大きくなったり、小さくなったりします。このフラフラの動き、ぶれの大きさを変動率（σ）で表わします。このぶれが大きいと、酔っ払いはなかなか帰宅できません。いつもなら１０分で帰れるところが３０分かかったりします。１０分後に酔っ払いがどこにいるのかは、偶然たどり着いた場所なので特定できませんが、家の近辺にいる可能性が最も高く、家から遠く離れている可能性は低くなります。こうした価格の現れ方（確率分布）をグラフにすると、釣鐘型のグラフになります。この確率分布を正規分布と呼んでいます。

 

 

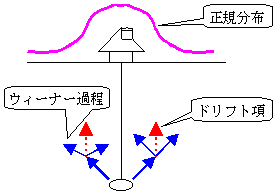
この「酔っ払いの千鳥足」の例えを、原資産の予測モデルにあてはめて説明してみましょう。

 

原資産価格が１日ごとに、上がるか下がるかという動きを繰り返すとします。仮に、１日の変化幅が１円であった場合、１００日間連続して上昇するとプラス１００円に、連続して下降するとマイナス１００円になります。原資産価格は、マイナス１００円からプラス１００円の価格帯に分布することになります。確率的には、上昇と下降を同程度（５０回　１００÷２＝５０）繰り返す場合が一番多いと予想できますから、価格が０円のところで終わる可能性が最も高くなります。この確率分布は、正規分布になります。

 

≪ウィーナー過程とドリフト項≫

 

「酔っ払いの千鳥足」の動きを数式（関数）で表わすと、基本的方向性を示す動きと確率的変動が合成されたものとなります。

 

 

ドリフト項は、原資産価格の期待収益率（予想平均収益率）を示します。ドリフト項は、グラフでいう直線の傾きに相当します。
ウィーナー過程は、ぶれの大きさである変動率と、標準正規分布からの無作為標本と、経過時間を掛け合わせたもので表わされます。
ドリフト項（基本的な方向性）をウィーナー過程に合わせたものを、一般化したウィーナ－過程といいます。

 

 

≪幾何ブラウン運動≫

 

価格幅でのブラウン運動を算術的ブラウン運動といいます。これに対して、何パーセントという変化率（価格比）でブラウン運動をすると仮定したものを幾何ブラウン運動といいます。金融の原資産価格はマイナスにはならないので、原資産価格の予測モデルには幾何ブラウン運動を用います。

 

原資産価格が、価格幅での変動を繰り返すと、計算上マイナスの数値となる場合があります。しかし、現実の原資産価格がマイナスになることはありません。これでは、予測モデルの原資産価格が、現実の原資産価格の動きと適合していないことになります。これは、変動の様子を価格幅（変化量）で捉えたことが原因です。

 

そこで、「価格幅」で変動するのではなく、「価格比（変化率）」で変動すると置き換えると、価格が下がり続けてもマイナスにならず、予測モデルは実際の動きに適合します。

 

 

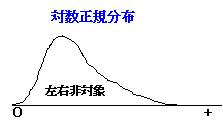
◆対数正規分布

 

算術的ブラウン運動の確率分布は、正規分布になります。一方、幾何ブラウン運動の確率分布は、対数正規分布になります。対数正規分布は、正の値をとる左右に歪んだ釣鐘型の分布です。原資産価格の対数である価格比（変化率）は、正規分布することになります。

 

対数

 

対数とは、大きな数字を指数に置き換えて表示したものです。例えば、１０００＝１０^３（１０の３乗）の場合には、３を「１０を底（テイ）とする１０００の対数」といい、３＝ｌｏｇ^１０１０００と表現します。
８＝２^３（２の３乗）の場合には、３を「２を底とする８の対数」といい、３＝ｌｏｇ^２８と表現します。

 

 

自然対数

 

底をｅ（ネピアの数（すう））にしたものを自然対数といいます。e＝２．７１８２８…で、ｌｏｇ^e　または、ｌｎ　という記号を使います。
「 ｘ＝ｌｏｇ^e株価」では、ｘという株価の対数が正規分布することを意味しています。

 

スポンサーリンク

金融大学TOP > よくわかる！金融用語辞典 > ウィーナー過程