
ミニ講座 IS-LMの計算
講師:有馬秀次
均衡国民所得を計算してみよう

ある国のマクロ経済モデルが次の式であたえられている。このときの均衡国民所得と均衡利子率を求めなさい。


この問題は、IS-LM分析モデルの計算問題です。
IS-LM分析は、ケインズの所得決定理論を説明するグラフ分析です。
グラフには、財市場の均衡(国民所得)を示すIS曲線と、貨幣市場の均衡(利子率)を示すLM曲線が描かれており、国民所得と利子率の関係をあらわしています。

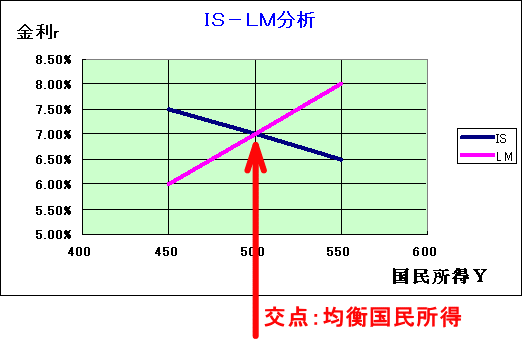
IS-LM分析のグラフでは、均衡国民所得はIS曲線とLM曲線の交点として示されます(国民所得を財市場と貨幣市場の同時均衡値として捉えます)。
したがって、均衡国民所得Yは、IS曲線式とLM曲線式を連立方程式として解くことで求められます。

※ここでは、IS曲線を数式であらわしたものをIS曲線式、LM曲線を数式であらわしたものをLM曲線式と呼びます。

① 問題から、IS曲線式とLM曲線式を求める
② 2式を連立させて、Yについて解く
① IS曲線式の導出
IS曲線は、財市場の均衡を示す曲線です。これを数式であらわしたものがIS曲線式で、「所得均衡式」によって求めることができます。
所得均衡式は、「Y=C+I+G」です。これにC式、I式、G式を代入して、IS曲線式を求めます。
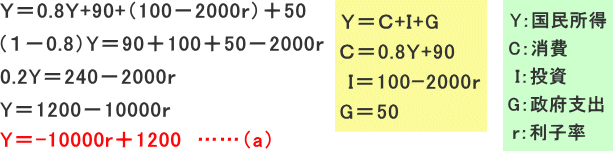
② LM曲線式の導出
LM曲線は、貨幣市場の均衡を示す曲線です。これを数式であらわしたものがLM曲線式で、貨幣市場均衡式である「貨幣総供給(M/P)=貨幣総需要(L)」によって求めることができます。
貨幣市場均衡式は、「M/P=L」です。これにL式を代入して、LM曲線式を求めます。
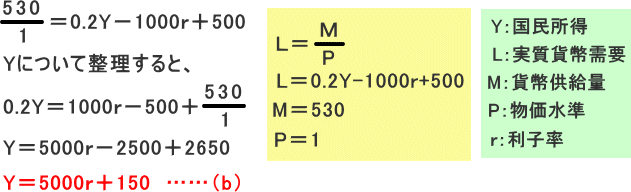
※実質貨幣総供給は、貨幣供給量Mを物価で割ったもので、M/Pであらわされます。
③ 連立方程式を解く

(a)式の左辺に、(b)式の右辺を代入します。
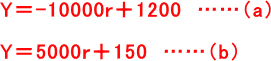
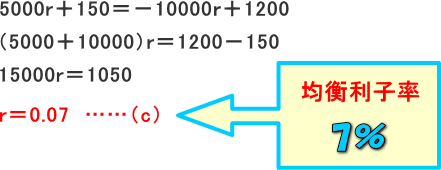
(c)式のr=0.07を(a)式に代入します。
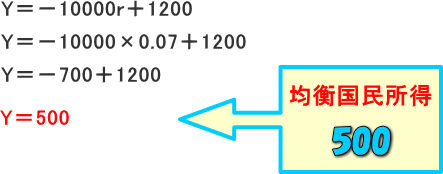

均衡国民所得は「Y=500」、均衡利子率は「r=0.07(7%)」となります。
均衡国民所得 Y=500
均衡利子率 r=0.07 (7%)

