
債券取引入門講座 第10回 イールドカーブ
講師:有馬秀次
1.イールドカーブとは何か
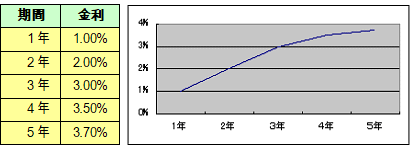
償還までの期間(残存年数)の異なる金利(利回り)を線で結んでグラフにしたものを、イールドカーブ(利回り曲線)と呼んでいます。縦軸に金利(利回り)、横軸に期間を目盛りにとったグラフです。
イールドカーブは、期間の長短が生み出す利回り(金利)と期間の関係を表わす「金利の期間構造(タームストラクチャー)」を分析するのに利用します。
2.パー・イールドとゼロ・クーポン・イールド
利回り(金利)は、パー・イールドとゼロ・クーポン・イールドという2種類の利回りに分けられます。
≪パー・イールド≫
パー・イールドとは、複利ベースの利付債の最終利回りのことです。利付債は、満期までの間に毎年一定の利子支払いが発生する金融商品です。
※最終利回りは、すでに発行されている債券を最終償還日まで所有した場合の利回りです。
買付価格が100円(パー)の利付債のパー・イールドは、償還差益が発生しないため、クーポンレートと一致します。したがって、パー・イールドのキャッシュ・フロー(期間別のお金の流れ)は、一般の貸付や金利スワップなどのキャッシュ・フローと共通しています。
パー・イールドを使って作ったグラフを、パー・イールド・カーブといいます。
≪ゼロ・クーポン・イールド≫
ゼロ・クーポン・イールドとは、複利ベ-スの割引債の最終利回りのことです。割引債は、満期日にのみキャッシュ・フローが発生する金融商品です。
ゼロ・クーポン・イールドは、信用度が同じであれば 各残存期間ごとに1つのレートしかないところから、金融商品の現在価値を決める際の物差しに利用されます。
ゼロ・クーポン・イールドのことを「スポット・レート」と呼んでいます。これは、現時点に始まるレートという意味で、フォワード・レート(先渡レート)と対比した呼び方です。
割引債のレートをグラフにしたものを、ゼロ・クーポン・イールド・カーブとか、スポット・レート・カーブといいます。金融資産の価格評価や金利の期間構造の分析に利用されています。そのため、単にイールドカーブというときは、ゼロ・クーポン・イールド・カーブのことを指します。

パー・イールド・カーブは、市場レートを使って作ることができますが、ゼロ・クーポン・イールド・カーブ(スポット・レート・カーブ)は、該当する期間の割引債のレートが得難いことから、直接作れないのが普通です。そこで、パー・イールドを使ってスポット・レートを推定することにしています。
3.パー・イールドの問題点
ここにクーポンレート5%の3年物の利付債と、クーポンレート7%の5年物の利付債があり、2つの債券を同時に100円で購入したとします。
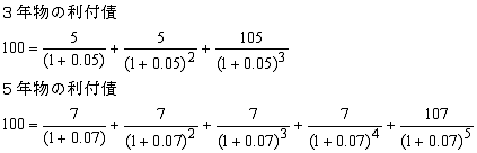
クーポンレートと償還元本というキャッシュ・フローを、残存期間に応じた最終利回り〔(1+最終利回り)^年数 〕で割り引いて合計すると、現時点での価値が計算できます。これを現在価値と呼んでいます。1年後に支払われる7円や、5年後に支払われる107円は、将来の時点に発生する価値なので将来価値と呼びます。
上記の債券の現在価値は、100円と計算されます。これは、債券の購入価格と一致します。

最終利回りを割引率に利用すると、期間に関係なく同じレートが使われることになります。3年債のキャッシュ・フローは5%で、5年債のキャッシュ・フローは7%で割り引かれています。
ここで2年目に支払われるクーポンレートの割引率に着目してみると、3年債のクーポンは5%で、5年債のクーポンは7%で割り引かれていることに気付きます。これは、同じ期間2年の将来価値を異なる割引レートで割り引いていることを示しています。
このパーレートを現在価値を求める際の尺度にすると、複数の金融商品の現在価値が比べられなくなってしまいます。そのため、現在価値の計算には、残存期間ごとに金利が1つしか存在しないスポット・レートが使われるのです。
4.スポット・レートの推定法
利付債の現在価値は、パー・イ-ルドで割り引いても、スポット・レートで割り引いても、等しくなければなりません。この関係を利用すると、推定するスポット・レートは、パーレートを使って推定することができます。

1年物の債券のゼロ・クーポン・イールドが1%、2年物の債券のパー・イールドが2%であったとします。2年物の債券の現在価値は、ゼロ・クーポン・イールドを使っても、パー・イールドを使っても等しいはずです。
下記の式で未知数は、期間2年のゼロ・クーポン・イールド r2 です。 この式を解くと r2は、2.01%と計算されます。
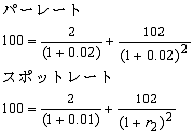
こうした計算を繰り返して、イールド・カーブを作成するのに必要な期間別のスポットレートのデータが推定されています。
5.イールド・カーブの形状
将来、金利が上がると予想される場合には、償還までの期間が長いほど、イールド・カーブが描き出す曲線は、右上がりになります。これを順イールドといいます。
金利が高くなる前に、長期間の借入れをしようとする人が増えるからです。
将来、金利が下がると予想される場合には、償還までの期間が長いほど、イールド・カーブが描き出す曲線は、右下がりになります。これを逆イールドといいます。
金利が低くなってから、長期間の借入れをしようとする人が増えるからです。

6.イールド・カーブの理論
イールドカーブ(金利の期間構造)がどのようにして決まるかを説明する、3つの仮説が知られています。

≪純粋期待仮説≫
純粋期待仮説は、長期金利は将来の金利の期待値で決定されるという理論です。これは、長期の金利で運用しても、短期の金利で運用しても、結果が同じになるように長期の金利が決められるという理論です。期待値(きたいち)とは、将来金利の予測値のことです。
例えば、現在の1年物の短期金利が10%であるとします。1年先に1年物の預金金利がいくらになっているのかはわかりませんが、現時点でこれを12%と予想するのであれば、2年物の長期金利は、約11%に決まるという理論です。 つまり、長期金利11%で2年間運用するのと、短期金利10%で1年間と1年先の短期金利12%で1年間運用した結果が等しくなるということを示しています。

1年物の将来金利が12%ではなく10%になった場合、100万円を1年物(10%)で借り入れて2年物(11%)で運用すれば、リスクなしで利益が得られることになります。
すると1年物(10%)で借り入れる人が増えるので、1年物の短期金利は上がります。同時に、2年物(11%)で運用する人が増えるので、2年物の長期金利は下がります。
こうした裁定取引(リスクなしに利益を得る取引)により、短期金利と長期金利の運用結果が等しくなるところで、金利が決定するという理論を純粋期待仮説といいます。
≪流動性プレミアム仮説≫
資金の運用期間が長くなるほど、将来に金利が変動して損失を被る可能性は、大きくなります。したがって、長期金利は、リスク分(不確実性)だけ短期金利よりも高くなるという仮説が成り立ちます。これを流動性プレミアム仮説といいます。
短期金利に上乗せされるリスク部分をリスク・プレミアムと呼んでいます。長期金利は、将来に対する不確実性が大きく、短期金利と比べて流動性がないため、その対価としてプレミアムがつくという考え方です。
≪市場分断仮説≫
短期金利と長期金利は、別々の市場で、各期間の金利に対する資金需給により決定されるという仮説です。純粋期待仮説で考えたような、短期市場と長期市場の間の裁定取引は行われないとする考え方です。
裁定取引を行うために発生する手数料が高かったり、市場に自由に参加できないような場合には、市場分断仮説が当てはまります。
◆参考

◆用語解説:キャッシュ・フロー
金融とはお金の貸借のことですが、時の上を流れるお金の流れと見ることもできます。お金の流れのことをキャッシュフローと呼んでいます。キャッシュフローは、金額、発生時期、受け払いの方向という要素から出来ています。金融商品のキャッシュフローは、複数のフローから構成されています。
例えば、購入価格90円の利付債(クーポンレート5%・残存期間3年)は、最初に90円を支払って、毎年5円ずつ受け取り、3年目に105円(額面+クーポンレート)を受け取るというフローで出来ています。

これを図にすると、下図のようになります。
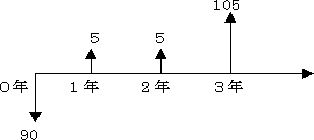
将来に発生するお金の流れには、どれくらいの価値があるのかわかりません。
上記の債券を例にすると、3年間に115円(5+5+105=115)が戻ってきます。これは、名目上の金額です。3年後に支払われる105円が現時点でどれくらいの価値があるのかわからないからです。
例えば、現在、銀行に100円を預金すれば利子がつきます。もし、預金金利が10%ならば、現在の100円は、3年後には133円になるはずです。
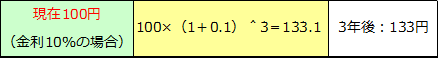
これを逆に考えると、3年後の133円は、現在では100円分の使い勝手しかないということになります。この100円を現在価値、3年後の133円を将来価値と呼びます。
将来価値から現在価値を求めるには、将来価値を運用利率で割り引けばよいのです。(この割引率は、金利に1が加えられていることに注意が必要です。)
上記の例では、金利は10%でしたから、1.1(1+0.1=1.1)で1年分ずつ割り引いて現在価値を計算しています。期間3年ならば、1.1で3回割り算をします。

現在価値を計算すれば、金融商品の価値を相互に比べることができます。異なるクーポン支払いが複数回発生する債券価値も、各々のクーポン価値を現在価値に引き直して合算すれば、債券の現在価値が計算されます。
現在価値の計算で重要なことは、割引率(スポットレート)がどれだけ妥当な金利であるかという点です。この割引率のとり方によって、現在価値は大きく変わってきます。スポットレートが現在価値を計算する際の尺度として使われているからです。
まとめ
パー・イールド
複利ベースの利付債の最終利回り
グラフにしたものを、パー・イールド・カーブという
ゼロ・クーポン・イールド
複利ベ-スの割引債の最終利回。スポット・レートともいう(フォワード・レートと対比)
グラフにしたものを、ゼロ・クーポン・イールド・カーブとか、スポット・レート・カーブという
順イールド
曲線は右上がり
将来、金利が上がると予想する人が多い
短期金利より長期金利が高くなる
逆イールド
曲線は右下がり
将来、金利が下がると予想する人が多い
短期金利より長期金利が低くなる
イールドカーブの理論
純粋期待仮説…長期金利は、将来の金利の期待値で決定される
流動性プレミアム仮説…長期金利は、短期金利よりも高くなる
市場分断仮説…短期金利と長期金利は、別々の市場で、各期間の金利に対する資金需給により決定される
問題と解答
- 残存年数の異なる金利を線で結んでグラフにしたものをイー●●カーブといい、「●●の期間構造」を分析するのに利用します。
- 利回りは、パー・イールドとゼロ・クーポン・イールドに分けられます。パー・イールドは複利ベースの●●債の最終利回りのことで、ゼロ・クーポン・イールドは複利ベ-スの●●債の最終利回りのことです。
- ●●債は、満期までの間に毎年一定の利子支払いが発生する金融商品です。一方、●●債は、満期日にのみキャッシュ・フローが発生する金融商品です。
- ゼロ・クーポン・イールドのことを、●●ット・レートといいます。これは、現時点に始まるレートという意味で、●●ワード・レート(先渡レート)と対比した呼び方です。
- パー・イールドを使って作ったグラフを●●・イールド・カーブといい、割引債のレートをグラフにしたものをゼロ・クーポン・イールド・カーブとか、●●ット・レート・カーブといいます。
- 金利が●がると予想される場合には、短期金利より長期金利が高くなり、イールド・カーブが描き出す曲線は右上がりになります。これを●イールドといいます。
- 金利が●がると予想される場合には、短期金利より長期金利が低くなり、イールド・カーブが描き出す曲線は右下がりになります。これを●イールドといいます。
- 純粋●●仮説は、長期金利が将来の金利の期待値で決定されるという理論です。短期金利と●●金利の運用結果が等しくなるところで、金利が決定するという考え方です。
- ●●性プレミアム仮説は、●●金利は将来に対する不確実性が大きく、短期金利と比べて流動性がないため、その対価としてプレミアムがつくという考え方です。
- 市場●●仮説は、短期金利と長期金利は、別々の市場で、各期間の金利に対する資金●●により決定されるという考え方です。
(答え)ルド、金利
(答え)利付、割引
(答え)利付、割引
(答え)スポ、フォ
(答え)パー、スポ
(答え)上、順
(答え)下、逆
(答え)期待、長期
(答え)流動、長期
(答え)分断、需給
