
オプション取引入門講座 第9回 ブラック・ショールズ・モデル
講師:有馬秀次
1.ブラック・ショールズ・モデル
ブラック・ショールズ・モデル(B&Sモデル)は、ヨーロピアンタイプ(満期日にのみ行使可能なオプション)のオプション価格を計算するモデルです。
計算に必要なデータ(株価、行使価格、期間、変動率、金利)は市場で入手できるうえ、計算にかかる時間が非常に短いという利点があるため、実務界で広く利用されています。
B&Sモデルは、1973年にアメリカのフィッシャー・ブラック(Fischer Black)とマイロン・ショールズ(Myron Scholes)が共同で発表し、ロバート・マートン(Robert C. Merton)によって証明されたオプション価格評価モデルです。
※1995年にフィッシャー・ブラックは亡くなりましたが、1997年にマイロン・ショールズとロバート・マートンはノーベル経済学賞を受賞しました。
2.汎用ブラック・ショールズ・モデル
B&Sモデルは、多くの学者によって他の原資産にも応用できるように研究されました。これらの各モデルを1つの計算式に集約したものを汎用ブラック・ショールズ・モデルと呼ぶことにします。
B&Sモデルは、配当支払いのない株式オプションのプレミアムを計算するモデルです。これに修正を加えると、広く一般の通貨、先物、債券等のオプションの計算ができるモデルに変えることができます。
その修正とは、B&Sモデルの原資産(株式)に配当支払いなど原資産が生み出す収益部分を考慮する計算項に置き換えるものです。B&S式のS(原資産)をe-qt・S(利回り調整済み原資産)に入れ替えることで、その計算ができます(ただし、q:原資産利回り)。
実務上、B&S式はこの修正されたモデル(汎用ブラック・ショールズ・モデル)で理解しておいた方が便利なので、このモデル式で説明していきます。


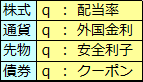

※B&SモデルのN(d1)はデルタ値(Δ)を意味しますが、汎用B&Sモデルではe-q・t・N(d1)がデルタ値(Δ)を意味します。オプションの原資産換算率を示し、ヘッジに必要な原資産金額を計算するのに利用します。
3.汎用ブラック・ショールズ式の計算
ブラックショールズの文字式には、見慣れない3種類の関数が入れ子になっています。この関数の値がわかれば、汎用B&Sモデルの計算は、掛け算と引き算だけの簡単な計算であることがわかります。
その関数とは、(1)指数関数 eーr・t (2)確率累積密度関数N(d) (3)自然対数Ln(s/k) の3つです。
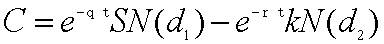
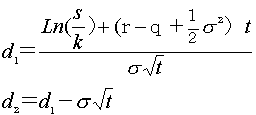
C:コールオプション価格 e :ネピアの数(すう) q :原資産利回り t :期間 S:原資産価格
N(d):標準正規分布の累積確率密度関数 r :安全利子率(非危険利子率) k :行使価格
d :累積密度関数N()の変数 σ:ボラティリティ(予想変動率)
(1)指数関数の計算
指数関数(ea)は、e (ネピアの数)をべき乗するという計算です。 e を a 乗しなさいという意味です。
e ≒2.7182 ですから、べき乗の計算機能がある計算機があれば簡単に計算することができますし、表計算ソフトのエクセルには、=exp( ) という関数が用意されています。
なお、e-a と指数にマイナスがついているものは、eaの逆数で 1/ea であることを示します。

◆金利調整項
金利調整項 e-r・tは、利回りや金利の調整項です。満期日のオプション価値を現在価値に引き直すための割引率の役割を果たしています。金利 e-r・tは、連続複利(複利ベースの金利の適用期間を無限に短くしたもの)での割引計算を行うことを意味します。
◆複利
複利とは、毎期ごとの元利合計額を新しい期の元本とする計算方法です。この計算期間を1年、半年、1カ月、1日、1秒と無限に短くして計算したときの複利金利が、 er・t で計算される連続複利金利です。これを逆数にしたものが割引係数 e-r・t です。 e-r・t は、単利に置き換えると1/(1+rt)を意味しています。
(2)確率累積密度関数の計算
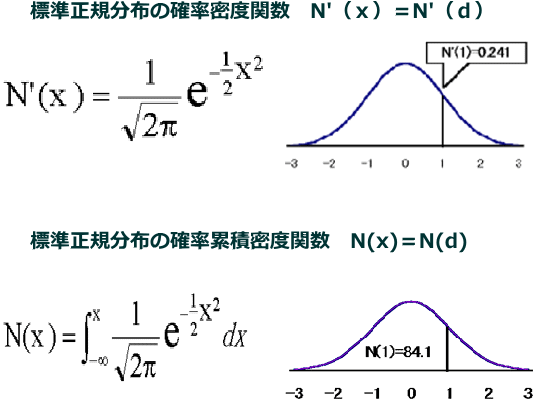
N(d)は、標準正規分布の確率累積密度関数で、ある事象の実現する確率を示しています。釣鐘型グラフの左端の-∞(マイナス無限大)からdまでの面積を表します。釣鐘型グラフ全体の面積を100%とした場合のd値までの実現する確率を示します。たとえば、N(1)は、84.1%となります。マイナス無限大から1までの面積が84.1%を占めることを意味します。N(d)は、一般にはN(x)と表記されています。
N(d)に似た関数で、N'(d)という関数があります。N'(d)は、標準正規分布の確率密度関数で標準正規分布のグラフを表します。N'(1)は、0.241というような値をとります。山の高さを表します。
この2つの関数は、親子関係にあります。N(d)という関数を微分するとN'(d)という関数になります。逆に、N'(x)という関数を積分するとN(x)になります。
確率累積密度関数N(d)を直接計算する方法はありません。理科年表の中の標準正規分布表から近似値を拾い出すのが1つの方法です。表計算ソフト(エクセル)を利用する場合には、=Normsdist( d ) を利用します。PC等でプログラムを書く場合には、近似式を利用します。
(3)自然対数の計算
自然対数 Ln は、ナチュラルロガリズムの略号で、e を底(てい)とする対数のことをいいます。これを自然対数と呼んでいます。
自然対数 Ln も直接計算する方法はありません。理科年表の中の対数表を利用して計算します。表計算ソフト(エクセル)では、 =Ln( ) という関数を利用します。
参考 : ウィーナー過程
4.ブラック・ショールズ式の計算手順
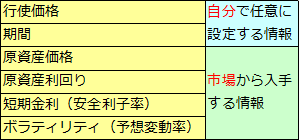
汎用ブラックショールズ式の計算には、行使価格、期間、原資産価格、原資産利回り、短期金利(安全利子率)、ボラティリティ(予想変動率)の6つの情報が必要です。
このうち、行使価格、期間の2つは、取引当事者が自分で任意に設定する情報です。一方、原資産価格、原資産利回り、短期金利、ボラティリティの4つは、市場から入手する情報です。
汎用B&Sモデルの計算は、3つのステップに分けると簡単になります。
(1)dの計算
d1 と d2を計算式から計算します。Ln(S/K)(自然対数)の計算には、表計算ソフトや計算機の関数機能を利用します。
(2)eの計算
金利 r と期間t から割引金利 e-q ・t 、e-r ・tを計算します。これも関数機能を利用します。関数機能がない場合には、e ≒ 2.7182として計算します。
(3)N()の計算
正規分布の累積密度関数 N(d1)、N(d2)を計算します。これも関数機能を利用します。関数機能がない場合には、近似式を利用します。
あとは答えを掛け合わせて、e-q ・t×S×N(d1)と、e-r ・t×K×N(d2)を計算して差額をとれば、コールプレミアムが計算されます。
プレミアム計算に必要な関数をすべて近似式で計算するのはむずかしいため、こうした計算は、コンピューターソフトの関数計算機能を利用します。表計算ソフトのロータス123やエクセルには、あらかじめこれらの関数が提供されているので、簡単にプレミアムを計算することができます。

5.ブラック・ショールズ式の意味
B&S式の意味を完全に理解するには高度な数学的知識が必要ですが、直感的なイメージで捉えることはそれほど難しくありません。大きくわけて、2通りの解釈で捉えることができます。
(1)危険資産への投資総額-借入総額
(2)※オプション行使日にイン・ザ・マネーである場合
受取予定である原資産の現在価値-支払予定である行使価格の現在価値
(1)オプション価格を、危険資産と安全資産の組み合わせコストから計算するという考え方です。オプションのキャッシュフローを、借入れ(安全資産)を使って原資産(危険資産)を購入することにより模倣します。その際に必要なコストとして、プレミアムが計算されるという考え方です。式の第一項(e-q・t×S×N(d1))は、この危険資産への投資額を示し、第二項(e-r・t×K×N(d2))は、安全資産への投資額(借入総額)を示すというものです。
(2)B&S式は、オプションの行使日に保有していると期待される本源的価値(S-K)を現在価値に直したものと考える方法です。オプション行使日にイン・ザ・マネーである場合に受け取れると期待される資産(S)の現在価値から、支払費用(K)の現在価値を差し引いたものと考えます。
6.ブラック・ショールズ・モデルの導出
B&Sモデルは、無裁定価格評価理論を使って偏微分方程式を作り、これを解いたモデルです。
まず、原資産価格の変動モデルとして、一般化したウィーナー過程を仮定します。次に、伊藤のレンマを使って、原資産の変動とオプションの変動を表わす関数を作ります。この関数を組み合わせて無裁定ポートフォリオを表わす方程式を作ります。その方程式を整理したものが、下記の偏微分方程式です。
この偏微分方程式を熱伝導方程式の解を使って解いたモデルがブラック・ショールズ・モデルです。このモデルを自力で導出するには、テーラー展開やフーリエ展開などの微積分の解法テクニックの知識が必要です。
偏微分方程式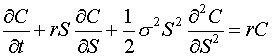
∂:ラウンド・ディ(偏微分を表わす記号)、 t :微小時間、
C:コールオプション価格、 r :安全金利(非危険利子率)、
S:原資産価格、 σ:シグマ(予想変動率)
◆伊藤のレンマ
伊藤のレンマとは、日本の数学者である伊藤清先生が確立した公式(伊藤の公式)です。
確率的に変動する変数があった場合に、その変数に依存する関数が従う過程がどうなるか、という確率微分方程式の法則性をみいだしたものです。オプションでは、原資産(株式)の関数の派生商品であるオプション関数が従う過程を表すのに利用しています。
まとめ
ブラック・ショールズ・モデル
ヨーロピアンタイプのオプション価格を計算するモデル
汎用ブラック・ショールズ・モデル
B&Sモデルに修正を加えると、他の原資産にも応用できるモデルに変わる。これらのモデルを1つの計算式に集約したもの
汎用ブラック・ショールズ式の計算
指数関数(ea)の計算…e (ネピアの数)を a 乗しなさいという意味。e ≒2.7182
確率累積密度関数の計算…表計算ソフト(エクセル)では、=Normsdist( d ) を利用します。
自然対数の計算…表計算ソフト(エクセル)では、 =Ln( ) を利用します。
ブラック・ショールズ式の計算手順
行使価格、期間、原資産価格、原資産利回り、短期金利(安全利子率)、ボラティリティ(予想変動率)、の6つの情報が必要
dの計算、eの計算、N()の計算、の3つのステップに分けると簡単に計算できる
ブラック・ショールズ式の意味
オプション価格を、危険資産と安全資産の組み合わせコストから計算するという考え方
オプションの行使日に保有していると期待される本源的価値を現在価値に直したものという考え方
ブラック・ショールズ・モデルの導出
無裁定価格評価理論を使って偏微分方程式を作り、これを解いたモデル
問題と解答
- B&Sモデルは、1973年にアメリカのフィッシャー・●●ックとマイロン・ショールズが共同で発表し、ロバート・マートンによって証明されたオプション●●評価モデルです。
- B&Sモデルは、配当支払いのない●●オプションのプレミアムを計算するモデルです。これに修正を加えると、広く一般の通貨、先物、債券等のオプションの計算ができるモデルに変えることができます。
- ●●関数 eーr・t 、確率累積密度関数N(d)、●●対数Ln(s/k) の3つの関数の値がわかれば、汎用B&Sモデルの計算は、掛け算と引き算だけの簡単な計算であることがわかります。
- ●●関数(ea)は、e (ネピアの数)をべき乗するという計算です。 e を a 乗しなさいという意味です。
e ≒2.●●82 ですから、べき乗の計算機能がある計算機があれば簡単に計算することができます。
- 確率密度関数N'(d)は、正規分布のグラフを表す●●関数です。この密度関数の面積を表す関数を●●累積密度関数N(d)といい、釣鐘型グラフの左端のマイナス無限大からdまでの面積を表しています。
- 自然●● Ln は、ナチュラルロガリズムの略号で、e を底とする対数のことをいいます。これを自然対数と呼んでいます。
- 汎用ブラックショールズ式の計算には、●●価格、期間、原資産価格、原資産利回り、短期●●(安全利子率)、ボラティリティ(予想変動率)の6つの情報が必要です。
- 行使価格、●●の2つは、取引当事者が自分で任意に設定する情報です。一方、原資産価格、原資産利回り、短期金利、ボラティリティの4つは、●●から入手する情報です。
- オプション価格を、危険資産と●●資産の組み合わせコストから計算するという考え方では、オプションのキャッシュフローを、借入れ(安全資産)を使って原資産(危険資産)を購入することにより模倣します。その際に必要なコストとして、●●ミアムが計算されるという考え方です。
- B&S式を、オプションの行使日に保有していると期待される本源的価値を●●価値に直したものと考える方法では、オプション行使日に●●・ザ・マネーである場合に受け取れると期待される資産の現在価値から、支払費用の現在価値を差し引いたものと考えます。
(答え)ブラ、価格
(答え)株式
(答え)指数、自然
(答え)指数、71
(答え)密度、確率
(答え)対数
(答え)行使、金利
(答え)期間、市場
(答え)安全、プレ
(答え)現在、イン
