
債券取引入門講座 第9回 単利と複利
講師:有馬秀次
1.利回り
利回りは、投資期間に得られた収益を投資元本で割った比率です。投資元本に対してどれだけの収益が得られたかという投資効率を判断することができます。利回りは、投資を行う際の重要な尺度です。
利回りの計算には、単利と複利という2つの異なる計算方法が使われています。債券の利回りにも、商品によって単利と複利の両方の利回りが使われています。
単位の異なる物差しで計算した利回りで投資の判断を行うと、誤った判断を下してしまいます。そのため、利回りを考える場合には、その計算ベースが何であるかを理解しておくことが重要になります。
≪単利≫
単利は、投資元本を変えないで利回りを計算する方法です。投資元本にのみ利子がつきます。
銀行に100万円を預金したとき、単利で10%の利子がつくとすると、1年目も2年目も10万円の利息がつきます。利回りは、100×0.1=10と計算されます。元本の100万円は、1年目も2年目も変わりません。
≪複利≫
複利は、前期の元利合計を今期の元本として計算する方法です。投資元本のほかに、途中で支払われる利子にも利子がつきます。
銀行に100万円を預金をしたとき、複利で10%の利子がつくとします。1年目の利子は、単利と同じく10万円(100×0.1=10)ですが、2年目の利子は、11万円(110×0.1=11)と計算されます。
当初の元本に、1年目に得られた利子10万円を繰み込んで、1年後の元本を110万円とします。
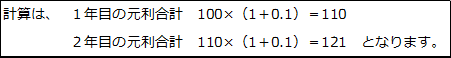
この銀行預金の元利合計は、2年後に121万円になります。
110を、100×(1+0.1)と書き換えると、121は、100×(1+0.1)×(1+0.1)と書くことができます。これを、100×(1+0.1)^2 と書くことにします。
^ は、べき乗の記号で、左の文字や数字を掛け合わせることを意味します。期間2年であれば、(1+0.1)を2回掛けるという意味で、(1+0.1)^2と書きます。
N年度の元利合計を計算する場合、(1+0.1)をn回掛ければよいのですから、N年後の元利合計は、次のように計算されます。
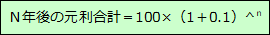
単利と複利の比較
≪現在価値と将来価値≫
ここで、現在の投資元本100万円を現在価値、2年後の元利合計121万円を将来価値と呼ぶことにします。
現在価値と将来価値との関係を、元利合計を求める計算式にあてはめてみます。元本という現在価値を複利利回りで運用すると、元利合計という将来価値が生みだされると見直すことができます。

逆に、将来価値を複利利回り10%で割り引くと、現在価値100万円が計算されます。

2.債券の利回り
債券の利回り計算にも、単利と複利の両方の利回りが使われています。
利回りの計算式は、覚えておく必要はありません。債券によって違った利回り基準が使われていることを理解していればよいのです。実際の計算は、関数電卓やコンピューターを使って計算できるからです。
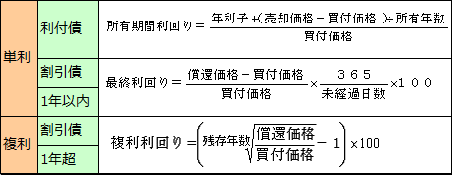
日本の債券の場合、利付債と期間1年以内の割引債は単利で、1年超の割引債は複利で計算しています。
それぞれの計算式は、以下のようになります。
欧米の債券は、利付債にも複利が利用されています。
ク-ポンの支払いが年2回ある場合には、半年を1期間として半年複利で計算しています。1年複利のレートに引き直す際に、米国とヨーロッパで異なる計算方法を採用しています。
欧州方式のことをAIBD(Association of International Bond Dealers)方式と呼ぶ場合もあります。
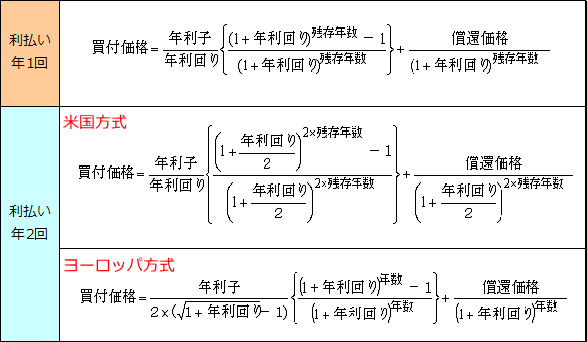
上記で紹介した計算式では、直接、年利回りを計算することはできまん。年利回りに任意の値を入れて、試行錯誤を繰り返して答えを求めます。
3.複利利回りの計算法
利回りを計算する方法として、2つの方法が利用されています。
1つは、等式を解く方法です。投資元本と、将来に回収される元利合計との関係を表す等式(左辺と右辺が等しい数式)を作り、それを解くことによって求める方法です。
(例)預金元本100万円で、2年後に元利合計が121万円になるとわかっている場合には、
100×(1+r )^2=121 という等式が作れます。これを r について解く方法です。
両辺を100で割って、 (1+r )^2=1.21
開平すると、 (1+r )=1.1
両辺から1を引くと、 r =0.1 となり、金利は10%と計算されます。
割引債の利回りの計算式は、この方法で導かれた計算式です。
もう1つの方法は、求める答えを推定して試行錯誤で答えを求める方法です。投資元本と元利合計の関係式が複雑になると、式を変形しても直接解けなくなります。
そうした場合には、求める答え(この場合、金利 r )に適当な数値を入れて左辺と右辺の値を計算し、2つの値を比べて推定し直すという方法を使います。こうして序々に答えに近づいていく方法です。
(例)定期預金の元本と元利合計がわかっていて利回りを知りたい場合、元本と元利合計の間には、次の等式が成り立ちます。
元本×(1+利回り)^2=元利合計
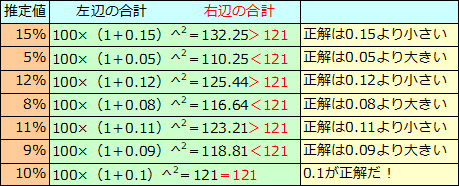
利回りを r として、r に任意の数字を入れていきます。
金利を r =0.15と推測して計算しはじめると、答えは132.25となって121より大きな数になってしまいます。これは、r が0.15より小さい数だということを示します。r =0.05と入れてみると、今度は110.25となって121より小さくなってしまいました。r は、5%より大きいことがわかります。
こうした計算を何回も繰り返して、やがて r を10%として計算した時点で正解だとわかります。
このように答えを収れんさせて求める方法です。
実際の計算は、関数電卓やコンピューターで行います。
最後に、上記で紹介した計算式がどのようにして求められるかを見てみることにしましょう。計算が苦手な方は飛ばしていただいて結構です。
≪1年超の割引債の利回り≫
買付価格と償還価格との間には、次の関係式が成り立ちます。

が導かれます。
≪年1回利付債の利回り≫
利付債の複利利回りは、直接求めることはできません。買付価格を求める計算式の利回りに任意の値を入れて収れんさせて答えを求めます。
買付価格と将来価値との関係を求める計算式を導きます。

≪年2回利払いの利付債≫
年に2回利払いがある利付債は、半年複利で計算します。
計算には、年1回利払いの計算式がそのまま使えます。半年を1期と考えて計算すればよいのです。ただし、求められる答えは、半年利回りになります。
この半年利回りを年利回りに引き直す際に、米国とヨーロッパで異なる方法を用いています。
年利回りを r、半年利回りを r' とするとき、米国方式では、r =2r' として計算するのに対し、ヨーロッパ方式では、r =(1+r' )^2-1 として計算します。
米国方式では、単利ベースで半年利回りを2倍したものと考えるのに対して、ヨーロッパ方式では、複利ベースで2乗したものと考える点の違いです。
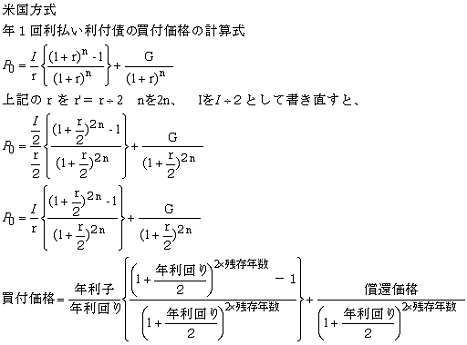
◆米国方式
r =2r' とすると r' = r ÷2 年1回利付債の買付価格を求める計算式の r を r' に置き換えて計算します。
ただし、1期間は半年ですから、n を 2n と置き換えます。
◆AIBD方式

参考 : 等比級数の和の公式
初項をa、公比をr、n項の和をSnとすると
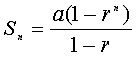
まとめ
単利
投資元本を変えないで利回りを計算する方法
投資元本にのみ利子がつく
複利
前期の元利合計を今期の元本として計算する方法
投資元本のほかに、途中で支払われる利子にも利子がつく
日本の債券
利付債と期間1年以内の割引債は単利
1年超の割引債は複利
欧米の債券
利付債にも複利を利用
米国方式とAIBD方式がある
利回りを計算する方法(2つ)
1.投資元本と、将来に回収される元利合計との関係を表す等式を解く方法
2.求める答えを推定して試行錯誤で答えを求める方法
問題と解答
- 利回りは、投資期間に得られた●●を投資元本で割った比率で、投資を行う際の重要な尺度です。利回りの計算には、単利と●●という2つの異なる計算方法が使われています。
- ●●は、投資元本を変えないで利回りを計算する方法です。投資●●にのみ利子がつきます。
- ●●は、前期の元利合計を今期の元本として計算する方法です。投資元本のほかに、途中で支払われる●●にも利子がつきます。
- 債券の利回り計算にも、単利と複利の両方の利回りが使われています。 日本の債券の場合、利付債と期間1年以内の割引債は●●で、1年超の割引債は●●で計算しています。
- 欧米の債券の場合、利付債にも複利が利用されます。クーポン支払が年2回である場合、●●とヨーロッパで異なる計算方法が採用されています。欧州方式のことを●●●●方式といいます。
- 利回りを計算する方法の1つは、●●を解く方法です。投資元本と、将来に回収される元利合計との関係を表す等式(左辺と右辺が等しい数式)を作り、それを解くことによって求める方法です。
- 利回りを計算する方法のもう1つは、求める答えを●●して試行錯誤で答えを求める方法です。求める答えに適当な数値を入れて左辺と右辺の値を計算し、2つの値を比べて推定し直すという方法です。
- ^ は、●●乗の記号で、左の文字や数字を掛け合わせることを意味します。N年度の元利合計を計算する場合、(1+0.1)をn回掛ければよいので、N年後の元利合計=100×(1+0.1)^nとなります。
- 利付債の●●利回りは、直接求めることはできません。買付価格を求める計算式の利回りに任意の値を入れて収れんさせて答えを求めます。
- 年に●回利払いがある利付債は、半年複利で計算します。計算には、年1回利払いの計算式がそのまま使えます。半年を1期と考えて計算すればよいのですが、求められる答えは、●●利回りになります。
(答え)収益、複利
(答え)単利、元本
(答え)複利、利子
(答え)単利、複利
(答え)米国、AIBD
(答え)等式
(答え)推定
(答え)べき
(答え)複利
(答え)2、半年
